时间序列分析工具箱——sweep

阅读量：4952 次

发布时间：2019-06-11

本文共 10025 字，大约阅读时间需要 33 分钟。

翻译自《Demo Week: Tidy Forecasting with sweep》

原文链接：www.business-science.io/code-tools/2017/10/25/demo_week_sweep.html

时间序列分析工具箱——sweep

`sweep` 的用途

正如 broom 包之于 stats 包，sweep 包用来简化使用 forecast 包的工作流。本教程将逐一介绍常用函数 sw_tidy、sw_glance、sw_augment 和 sw_sweep 的用法。

sweep 和 timetk 带来的额外好处是，如果 ts 对象是由 tbl 对象转换来的，那么在预测过程中日期和时间信息会以 timetk 索引的形式保留下来。一句话概括：这意味着我们最终可以在预测时使用日期，而不是 ts 类型数据使用的规则间隔数字日期。

加载包

本教程要使用到四个包：

sweep：简化 forecast 包的使用

forecast：提供 ARIMA、ETS 和其他流行的预测算法

tidyquant：获取数据并在后台加载 tidyverse 系列工具

timetk：时间序列数据处理工具，用来将 tbl 转换成 ts

# Load librarieslibrary(sweep)      # Broom-style tidiers for the forecast packagelibrary(forecast)   # Forecasting models and predictions packagelibrary(tidyquant)  # Loads tidyverse, financial pkgs, used to get datalibrary(timetk)     # Functions working with time series

数据

我们使用 timetk 教程中数据——，用 tidyquant 中的 tq_get() 函数从 FRED 获取。

# Beer, Wine, Distilled Alcoholic Beverages, in Millions USDbeer_sales_tbl <- tq_get(    "S4248SM144NCEN",    get = "economic.data",    from = "2010-01-01",    to = "2016-12-31")beer_sales_tbl

## # A tibble: 84 x 2##          date price##        
     
     
      ##  1 2010-01-01  6558##  2 2010-02-01  7481##  3 2010-03-01  9475##  4 2010-04-01  9424##  5 2010-05-01  9351##  6 2010-06-01 10552##  7 2010-07-01  9077##  8 2010-08-01  9273##  9 2010-09-01  9420## 10 2010-10-01  9413## # ... with 74 more rows

可视化数据是一个好东西，这有助于帮助我们了解正在使用的是什么数据。可视化对于时间序列分析和预测尤为重要。我们将使用 tidyquant 画图工具：主要是用 geom_ma(ma_fun = SMA，n = 12) 来添加一个周期为 12 的简单移动平均线来了解趋势。我们还可以看到似乎同时存在着趋势性（移动平均线以近似线性的模式增长）和季节性（波峰和波谷倾向于在特定月份发生）。

# Plot Beer Salesbeer_sales_tbl %>%    ggplot(aes(date, price)) +    geom_line(col = palette_light()[1]) +    geom_point(col = palette_light()[1]) +    geom_ma(ma_fun = SMA, n = 12, size = 1) +    theme_tq() +    scale_x_date(date_breaks = "1 year", date_labels = "%Y") +    labs(title = "Beer Sales: 2007 through 2016")

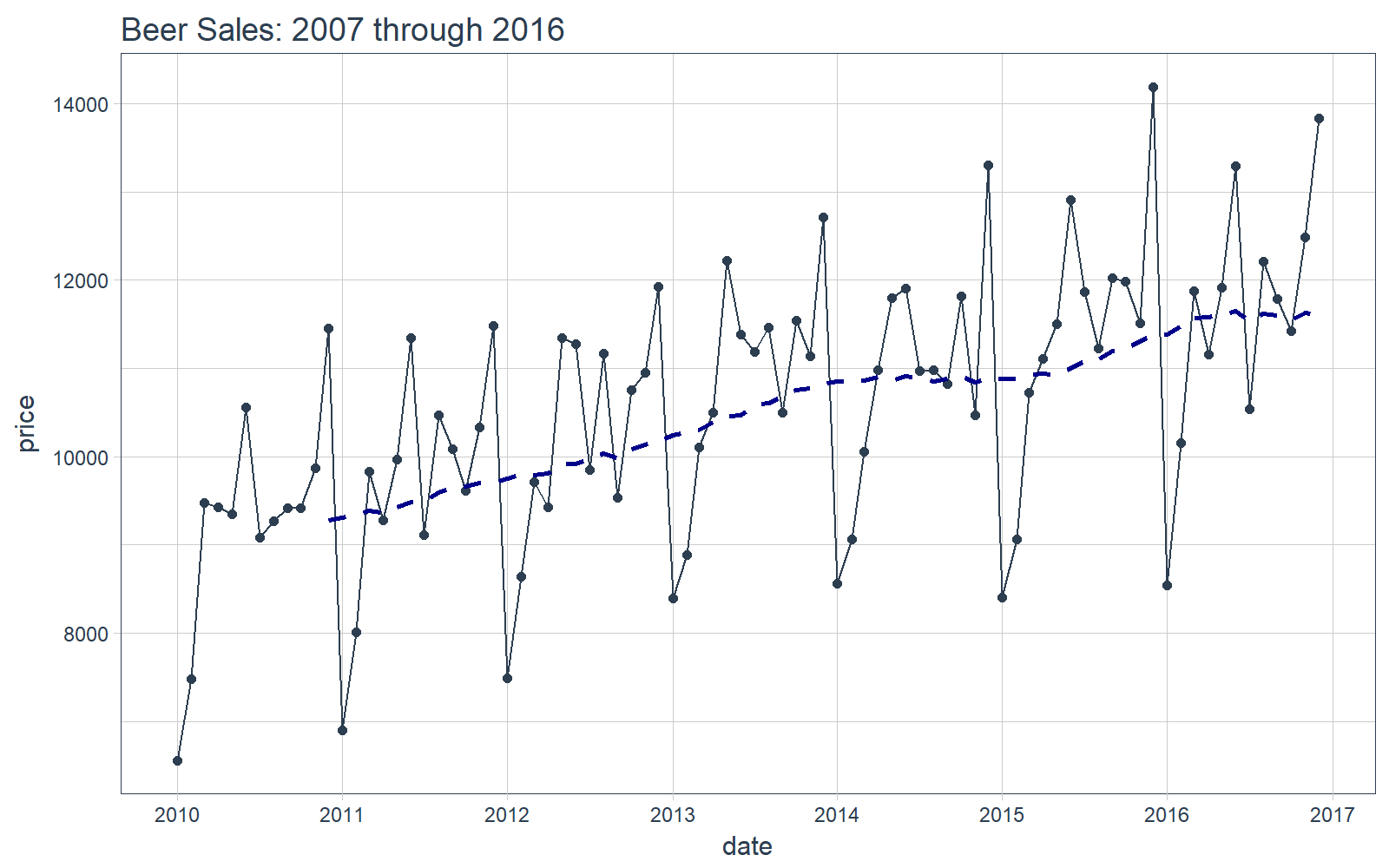
现在你对我们要分析的时间序列有了直观的感受，那么让我们继续！

Demo：`forecast` + `sweep` 的简化预测工作流

我们将联合使用 forecast 和 sweep 来简化预测分析。

关键想法：使用 forecast 包做预测涉及到 ts 对象，用起来并不简洁。对于 stats 包来说有 broom 来简化使用；forecast 包就用 sweep。

目标：我们将用 ARIMA 模型预测未来 12 个月的数据。

STEP 1：创建 `ts` 对象

使用 timetk::tk_ts() 将 tbl 转换成 ts，从之前的教程可以了解到这个函数有两点好处：

这是一个统一的方法，实现与 ts 对象的相互转换。

得到的 ts 对象包含 timetk_idx 属性，是一个基于初始时间信息的索引。

下面开始转换，注意 ts 对象是规则时间序列，所以要设置 start 和 freq。

# Convert from tbl to tsbeer_sales_ts <- tk_ts(    beer_sales_tbl,    start = 2010,    freq = 12)beer_sales_ts

##        Jan   Feb   Mar   Apr   May   Jun   Jul   Aug   Sep   Oct## 2010  6558  7481  9475  9424  9351 10552  9077  9273  9420  9413## 2011  6901  8014  9833  9281  9967 11344  9106 10468 10085  9612## 2012  7486  8641  9709  9423 11342 11274  9845 11163  9532 10754## 2013  8395  8888 10109 10493 12217 11385 11186 11462 10494 11541## 2014  8559  9061 10058 10979 11794 11906 10966 10981 10827 11815## 2015  8398  9061 10720 11105 11505 12903 11866 11223 12023 11986## 2016  8540 10158 11879 11155 11916 13291 10540 12212 11786 11424##        Nov   Dec## 2010  9866 11455## 2011 10328 11483## 2012 10953 11922## 2013 11139 12709## 2014 10466 13303## 2015 11510 14190## 2016 12482 13832

检查 ts 对象具有 timetk_idx 属性。

# Check that ts-object has a timetk indexhas_timetk_idx(beer_sales_ts)

## [1] TRUE

OK，这对后面要用的 sw_sweep() 很重要。下面我们就要建立 ARIMA 模型了。

STEP 2A：ARIMA 模型

我们使用 forecast 包里的 auto.arima() 函数为时间序列建模。

# Model using auto.arimafit_arima <- auto.arima(beer_sales_ts)fit_arima

## Series: beer_sales_ts ## ARIMA(3,0,0)(1,1,0)[12] with drift ## ## Coefficients:##           ar1     ar2     ar3     sar1    drift##       -0.2498  0.1079  0.6210  -0.2817  32.1157## s.e.   0.0933  0.0982  0.0925   0.1333   5.8882## ## sigma^2 estimated as 175282:  log likelihood=-535.49## AIC=1082.97   AICc=1084.27   BIC=1096.63

STEP 2B：简化模型

就像 broom 简化 stats 包的使用一样，我么可以使用 sweep 的函数简化 ARIMA 模型。下面介绍三个函数：

sw_tidy()：用于检索模型参数

sw_glance()：用于检索模型描述和训练集的精确度度量

sw_augment()：用于获得模型残差

`sw_tidy`

sw_tidy() 函数以 tibble 对象的形式返回模型参数。

# sw_tidy - Get model coefficientssw_tidy(fit_arima)

## # A tibble: 5 x 2##    term   estimate##   
          
     
      ## 1   ar1 -0.2497937## 2   ar2  0.1079269## 3   ar3  0.6210345## 4  sar1 -0.2816877## 5 drift 32.1157478

`sw_glance`

sw_glance() 函数以 tibble 对象的形式返回训练集的精确度度量。可以使用 glimpse 函数美化显示结果。

# sw_glance - Get model description and training set accuracy measuressw_glance(fit_arima) %>%    glimpse()

## Observations: 1## Variables: 12## $ model.desc 
    
      "ARIMA(3,0,0)(1,1,0)[12] with drift"## $ sigma      
     
       418.6665## $ logLik     
      
        -535.4873## $ AIC        
       
         1082.975## $ BIC        
        
          1096.635## $ ME         
         
           1.189875## $ RMSE 
          
            373.9091## $ MAE 
           
             271.7068## $ MPE 
            
              -0.06716239## $ MAPE 
             
               2.526077## $ MASE 
              
                0.4989005## $ ACF1 
               
                 0.02215405

`sw_augument`

sw_augument() 函数返回的 tibble 表中包含 .actual、.fitted 和 .resid 列，有助于在训练集上评估模型表现。注意，设置 timetk_idx = TRUE 返回初始的日期索引。

# sw_augment - get model residualssw_augment(fit_arima, timetk_idx = TRUE)

## # A tibble: 84 x 4##         index .actual   .fitted    .resid##        
       
          
           
       
        ##  1 2010-01-01    6558  6551.474  6.525878##  2 2010-02-01    7481  7473.583  7.416765##  3 2010-03-01    9475  9465.621  9.378648##  4 2010-04-01    9424  9414.704  9.295526##  5 2010-05-01    9351  9341.810  9.190414##  6 2010-06-01   10552 10541.641 10.359293##  7 2010-07-01    9077  9068.148  8.852178##  8 2010-08-01    9273  9263.984  9.016063##  9 2010-09-01    9420  9410.869  9.130943## 10 2010-10-01    9413  9403.908  9.091831## # ... with 74 more rows

我们可以可视化训练数据上的残差，看一下数据中有没有遗漏的模式没有被发现。

# Plotting residualssw_augment(fit_arima, timetk_idx = TRUE) %>%    ggplot(aes(x = index, y = .resid)) +    geom_point() +     geom_hline(yintercept = 0, color = "red") +     labs(title = "Residual diagnostic") +    scale_x_date(date_breaks = "1 year", date_labels = "%Y") +    theme_tq()

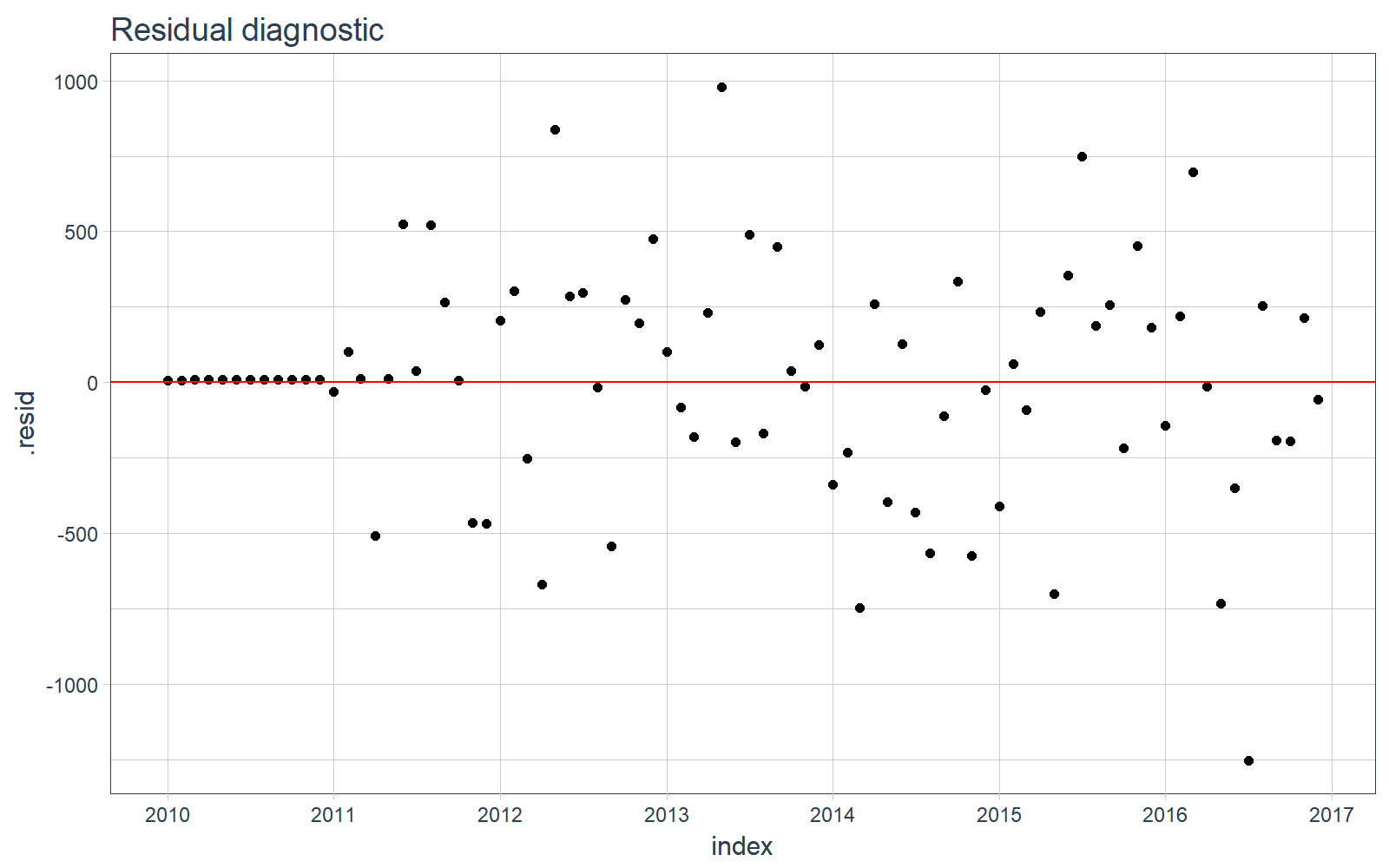
STEP 3：预测

使用 forecast() 函数做预测。

# Forecast next 12 monthsfcast_arima <- forecast(fit_arima, h = 12)

一个问题是，预测结果并不“tidy”。我们需要数据框形式的预测结果，以便应用 tidyverse 的功能，然而预测结果是 forecast 类型的，一种基于 ts 的对象。

class(fcast_arima)

## [1] "forecast"

STEP 4：用 `sweep` 简化预测

我们使用 sw_sweep() 简化预测结果，一个额外的好处是，如果 forecast 对象有 timetk 索引，我们可以用它返回一个日期时间索引，不同于 ts 对象的规则索引。

首先要确认 forecast 对象有 timetk 索引，这需要在使用 sw_sweep() 时设置 timetk_idx 参数。

# Check if object has timetk index has_timetk_idx(fcast_arima)

## [1] TRUE

现在，使用 sw_sweep() 来简化预测结果，它会在内部根据 time_tk 构造一条未来时间序列索引（这一步总是会被执行，因为我们在第 1 步中用 tk_ts() 构造了 ts 对象）注意：这意味着我们最终可以在 forecast 包中使用日期（不同于 ts 对象中的规则索引）！。

# sw_sweep - tidies forecast outputfcast_tbl <- sw_sweep(fcast_arima, timetk_idx = TRUE)fcast_tbl

## # A tibble: 96 x 7##         index    key price lo.80 lo.95 hi.80 hi.95##        
      
      
       
        
         
          
          
           ## 1 2010-01-01 actual 6558 NA NA NA NA## 2 2010-02-01 actual 7481 NA NA NA NA## 3 2010-03-01 actual 9475 NA NA NA NA## 4 2010-04-01 actual 9424 NA NA NA NA## 5 2010-05-01 actual 9351 NA NA NA NA## 6 2010-06-01 actual 10552 NA NA NA NA## 7 2010-07-01 actual 9077 NA NA NA NA## 8 2010-08-01 actual 9273 NA NA NA NA## 9 2010-09-01 actual 9420 NA NA NA NA## 10 2010-10-01 actual 9413 NA NA NA NA## # ... with 86 more rows

STEP 5：比较真实值和预测值

我们可以使用 tq_get() 来检索实际数据。注意，我们没有用于比较的完整数据，但我们至少可以比较前几个月的实际值。

actuals_tbl <- tq_get(    "S4248SM144NCEN",    get = "economic.data",    from = "2017-01-01",    to = "2017-12-31")

注意，预测结果放在 tibble 中，可以方便的实现可视化。

# Visualize the forecast with ggplotfcast_tbl %>%    ggplot(        aes(x = index, y = price, color = key)) +    # 95% CI    geom_ribbon(        aes(ymin = lo.95, ymax = hi.95),         fill = "#D5DBFF", color = NA, size = 0) +    # 80% CI    geom_ribbon(        aes(ymin = lo.80, ymax = hi.80, fill = key),         fill = "#596DD5", color = NA,         size = 0, alpha = 0.8) +    # Prediction    geom_line() +    geom_point() +    # Actuals    geom_line(        aes(x = date, y = price), color = palette_light()[[1]],        data = actuals_tbl) +    geom_point(        aes(x = date, y = price), color = palette_light()[[1]],         data = actuals_tbl) +    # Aesthetics    labs(        title = "Beer Sales Forecast: ARIMA", x = "", y = "Thousands of Tons",        subtitle = "sw_sweep tidies the auto.arima() forecast output") +    scale_x_date(        date_breaks = "1 year",        date_labels = "%Y") +    scale_color_tq() +    scale_fill_tq() +    theme_tq()

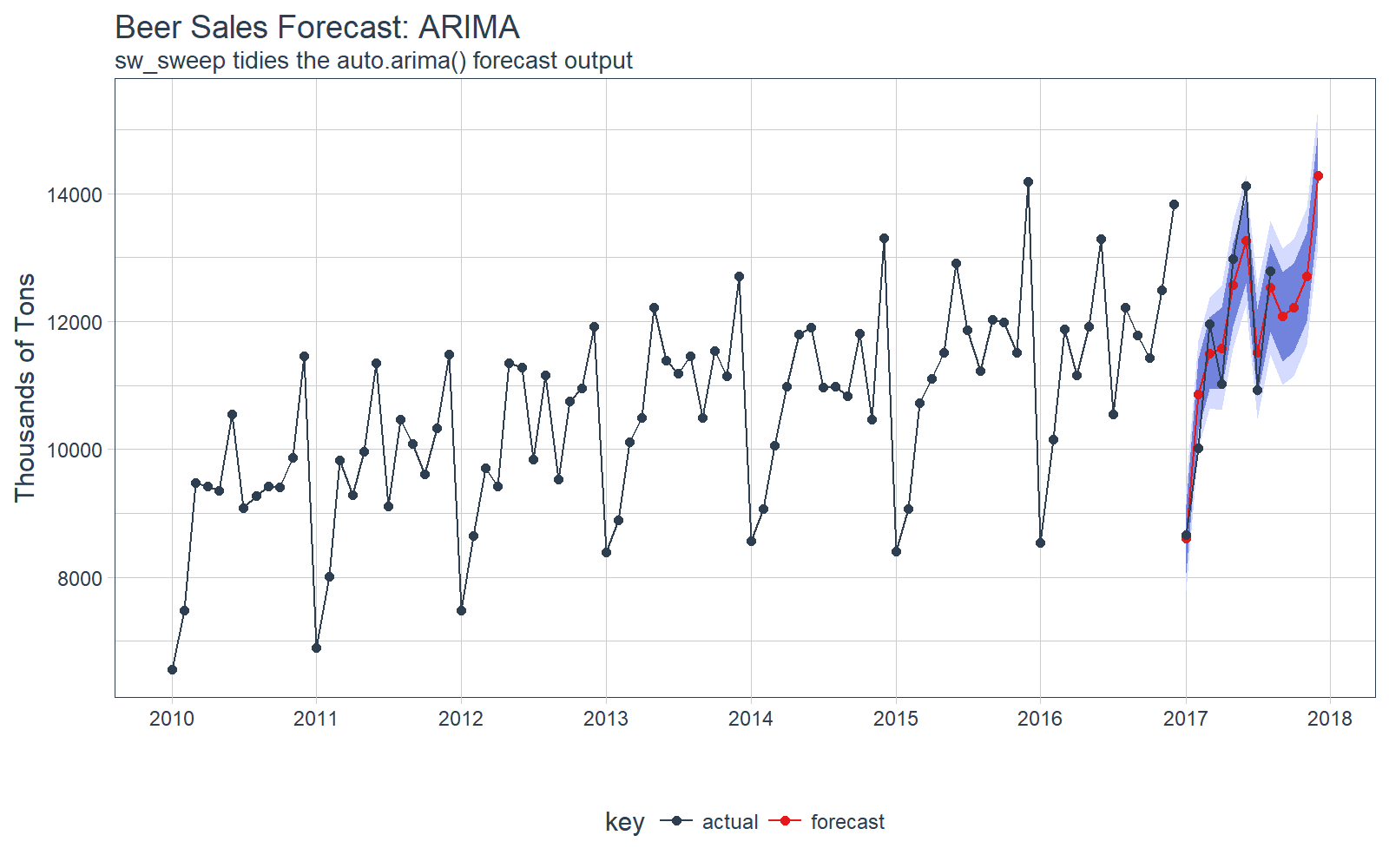
我们可以研究测试集上的误差（真实值 vs 预测值）。

# Investigate test error error_tbl <- left_join(    actuals_tbl,    fcast_tbl,    by = c("date" = "index")) %>%    rename(        actual = price.x, pred = price.y) %>%    select(date, actual, pred) %>%    mutate(        error     = actual - pred,        error_pct = error / actual)         error_tbl

## # A tibble: 8 x 5##         date actual      pred      error    error_pct##       
      
          
            
               
        
         ## 1 2017-01-01   8664  8601.815   62.18469  0.007177365## 2 2017-02-01  10017 10855.429 -838.42908 -0.083700617## 3 2017-03-01  11960 11502.214  457.78622  0.038276439## 4 2017-04-01  11019 11582.600 -563.59962 -0.051147982## 5 2017-05-01  12971 12566.765  404.23491  0.031164514## 6 2017-06-01  14113 13263.918  849.08191  0.060163106## 7 2017-07-01  10928 11507.277 -579.27693 -0.053008504## 8 2017-08-01  12788 12527.278  260.72219  0.020388035

并且，我们可以做简单的误差度量。MAPE 接近 4.3%，比简单的略好一点，但是 RMSE 变差了。

# Calculate test error metricstest_residuals <- error_tbl$errortest_error_pct <- error_tbl$error_pct * 100 # Percentage errorme   <- mean(test_residuals, na.rm=TRUE)rmse <- mean(test_residuals^2, na.rm=TRUE)^0.5mae  <- mean(abs(test_residuals), na.rm=TRUE)mape <- mean(abs(test_error_pct), na.rm=TRUE)mpe  <- mean(test_error_pct, na.rm=TRUE)tibble(me, rmse, mae, mape, mpe) %>%    glimpse()

## Observations: 1## Variables: 5## $ me   
    
      6.588034## $ rmse 
     
       561.4631## $ mae  
      
        501.9144## $ mape 
       
         4.312832## $ mpe  
        
          -0.3835956